ENGDUINO LIBRARIES: THE ACCELEROMETER

The accelerometer on the Engduino measures accelerations, as its name suggests. Again, the

interface is straightforward. As it is set up, the accelerometer can measure accelerations of ±2g.

• HEADER

At the top of your program you must have the following line.

#include <EngduinoAccelerometer.h>
#include <Wire.h>

NOTE the extra include.

• SETUP()

At the top of your program you must have the following line.

EngduinoAccelerometer.begin();

• BASIC FUNCTIONS

The accelerometer reads three dimensions of acceleration, returns three values and these are stored in an array. The values of acceleration are given in ‘g’ (where 1g is the acceleration due to gravity).

void loop() {
float accelerations[3];
EngduinoAccelerometer.xyz(accelerations);
float x = accelerations[0];
float y = accelerations[1];
float z = accelerations[2];
Serial.print("Acceleration: x = ");
Serial.print(x);
Serial.print("g y = ");
Serial.print(y);
Serial.print("g z = ");
Serial.print(z);
Serial.println("g");
delay(1000);
}

Upload this and open the serial monitor. Hold the Engduino flat with the LEDs uppermost. You

should see that the X and Y accelerations are near to zero, and the Z acceleration is close to ‐1. This

tells you that gravity is acting downwards relative to the Engduino. Flip the board over so the LEDs

are nearest the floor. The Z value should become positive at +1g. Work out which axis represents X

and which represents Y (hint: turn the Engduino on its side and on its end).

If you shake the Engduino vigorously enough, you’ll see that the accelerations go up to ±2g. That’s

because this accelerometer is set to measure a maximum of ±2g: the true number might be higher

than that.

• MORE ADVANCED FUNCTIONS

There aren’t any for the accelerometer. But the 3D acceleration is what is known as a vector

quantity (talk to your maths teacher) – it has a magnitude (size, length) and a direction. To get the

overall magnitude, irrespective of orientation, we need to do a bit of maths. If we only had X and Y

axes (i.e. we had a 2D accelerometer) the situation would be:

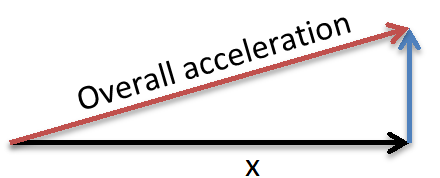
We can calculate the magnitude (length) of the resultant from Pythagoras’ rule:

$$ acceleration = √(x²+y²)

$$

BUT, we have a 3D accelerometer – and the same principle holds where we have X, Y and Z axes. So

the overall magnitude of the resultant acceleration vector is:

$$ acceleration = √(x²+y²+z²)

$$

Add the following to the code above:

float a = sqrt(x*x + y*y + z*z);
Serial.print("Acceleration: = ");
Serial.println(a);

Now, if you keep the accelerometer still (put it on the desk), this will give an acceleration of about

1g, irrespective of what orientation you have the Engduino in – and it will be different to that as you

move it about. Actually, the value will vary slightly even if you keep it still, because the

accelerometer isn’t a perfect measuring device. Dealing with this is a process called calibration and is

something we have to do when we need to know a quantity accurately.

See if you can change the colour of the LEDs depending on the direction of the acceleration.